Niveau et Durée :

Spécialité Maths en classe de première - une séquence (7 heures).

Présentation et objectifs :

Séquence complète pour introduire le nombre dérivé et la fonction dérivée. Dans cette séquence, plusieurs dispositifs pédagogiques ont été testés : Méthode JIGSAW, différenciation, démonstration. De plus, l’espace pédagogique de l’établissement a été utilisé comme espace de dépôt des fichiers, comme support. L’intégralité de cette séquence peut se faire sans utiliser l’espace pédagogique avec seulement les fiches papiers.

→ Vous trouverez en base de cette page, tous les documents utiles pour une utilisation en classe après une appropriation si besoin.

Dans les programmes du niveau visé :

Connaissances

Point de vue local :

• Taux de variation. Sécantes à la courbe représentative d’une fonction en un point donné.
• Nombre dérivé d’une fonction en un point, comme limite du taux de variation. Notation .
• Tangente à la courbe représentative d’une fonction en un point, comme « limite des sécantes ». Pente.
• Équation : la tangente à la courbe représentative de f au point d’abscisse a est la droite d’équation y=f’(a)(x-a)+f(a)
• Fonction dérivable sur un intervalle. Fonction dérivée.

Point de vue global :

• Fonction dérivée des fonctions carré, cube, inverse, racine carrée.
• Pour entier naturel n, fonction dérivée de la fonction x^n.
• Fonction dérivée d’une somme.

Capacités associées

• Calculer un taux de variation, la pente d’une sécante.
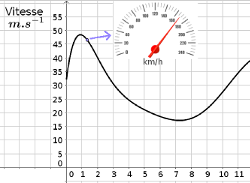
• Interpréter le nombre dérivé en contexte : pente d’une tangente, vitesse instantanée.
• Déterminer graphiquement un nombre dérivé par la pente de la tangente. Construire la tangente en un point à une courbe représentative connaissant le nombre dérivé.
• Déterminer l’équation de la tangente en un point à la courbe représentative d’une fonction.
• À partir de la définition, calculer le nombre dérivé en un point ou la fonction dérivée de la fonction carré, de la fonction inverse.
• Dans des cas simples, calculer une fonction dérivée en utilisant les propriétés des opérations sur les fonctions dérivables (« u + v » et « k u  »)

Remarque : Cette séquence est à compléter par une deuxième séquence en décalée qui permettra de travailler les autres connaissances et capacités associées sur la dérivation mentionnées dans les programmes.

SITOGRAPHIE :

Groupe Jigsaw de l’IREM de Rennes https://jigsawirem.wixsite.com/jigsaw-mathematiques Le Jigsaw-teaching ou “coopération puzzle” est un dispositif d’enseignement de type groupe visant à favoriser à la fois l’autonomie dans l’apprentissage, l’expertise et la coopération des élèves.

Description des documents à télécharger ci-dessous :

• La fiche professeur complète qui décrit notamment entièrement le déroulement de la séquence.
• Un premier dossier zippé contient tous les documents relatifs à la mise en place du JIGSAW du début de la séquence.
• Un deuxième dossier zippé contient les fiches complémentaires (COURS et EXERCICES).

Conception : Groupe de production lycée - 2020